点分治
在说点分治之前先说一下序列分治,序列分治大家都知道吧,就是把序列从某个位置(一般是中间点)分成两部分,统计跨越两部分的答案再递归处理两部分。树的点分治的道理和序列分治很像,但树没有中点,该怎么分治呢?再对比序列分治,序列相当于一条链,而序列的中点就是这条链的重心,那么树的分治点就可以是这棵树的重心。回顾一下重心的性质:以树的重心为根,这棵树最大子树大小不大于整棵树大小的一半。这样就可以保证时间复杂度是O(nlogn),因为每次处理的树的大小都至少会减半,所以一个点从开始点分治到以这个点为分治重心最多logn层,也就是会被遍历logn次。
当以一个点为当前重心时,处理的答案是跨区域的(也就是统计任意两个子树之间经过重心产生的答案)。在这里介绍两种常用的统计方法:
1、统计所有子树中任意两点满足的方案数(不管两个点是否在同一棵子树里),再用单步容斥减掉在同一棵子树中的答案数。但这种方法的前提条件是统计答案满足逆运算(即总答案-不符合答案=符合答案)。
2、将当前子树里的点和之前遍历的子树中的所有点统计答案,这样避免了不符合的答案,也不需要满足逆运算,有的题只能用这种方法来统计。
最后说一下点分治题求解的主要过程:
1、找重心并以重心为根对子树dfs统计答案信息(例如路径长或者满足条件节点数)。
2、统计答案。
3、递归分治处理每棵子树。
代码时间
找重心
void getroot(int x,int fa){ size[x]=1; mx[x]=0; for(int i=head[x];i;i=next[i]) { if(to[i]!=fa&&!vis[to[i]]) { getroot(to[i],x); size[x]+=size[to[i]]; mx[x]=max(mx[x],size[to[i]]); } } mx[x]=max(mx[x],num-size[x]); if(!root||mx[x] 分治过程
void partition(int x){ vis[x]=1; ans+=calc(x,0); for(int i=head[x];i;i=next[i]) { if(!vis[to[i]]) { ans-=calc(to[i],val[i]); num=size[to[i]]; root=0; getroot(to[i],0); partition(root); } }} 通过代码可以发现这里找下一层重心时,联通块大小用的是上一层记录的子树大小,这样理论上来说找的并不是真的重心,但复杂度却是正确的,证明参见:
变量名解释:
size[i],i的子树大小;mx[i],以i为联通块的根时最大子树大小;num,当前联通块大小;mx[0]初始成INF。
推荐练习题:
BZOJ2599Race
BZOJ1316树上的查询
BZOJ4016最短路径树问题
BZOJ4182Shopping
BZOJ3451Normal
BZOJ3672购票
动态点分治
什么是动态点分治?就是对于树上信息进行修改并在每次修改后询问一些树上问题。对于这类带动态修改的问题,我们的思路一般就是用数据结构来维护一些在询问时需要的信息并使它们能够快速修改并查询。动态点分治同样是这种思路,不过它引入了一种新的数据结构(其实也不完全算数据结构)——点分树。
点分树就是在递归分治时将这一层的分治中心连向上一层的分治中心作为这一层分治中心的父节点所形成的新树,因为从开始点分治到以当前点为分治中心最多递归logn层,所以点分树的树高要小于等于logn。形象一点地描述点分树的构建如下图所示。
原树:
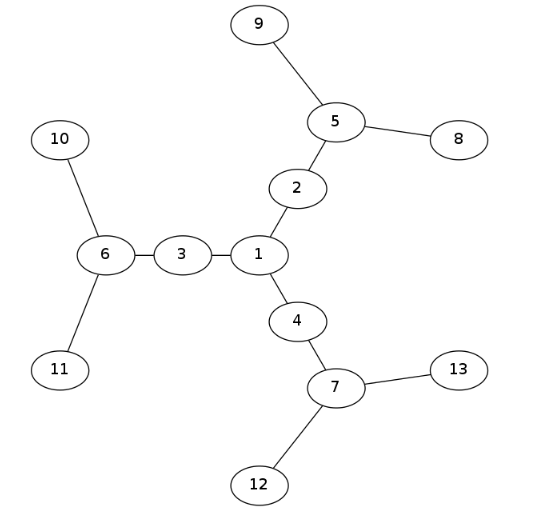
点分树:
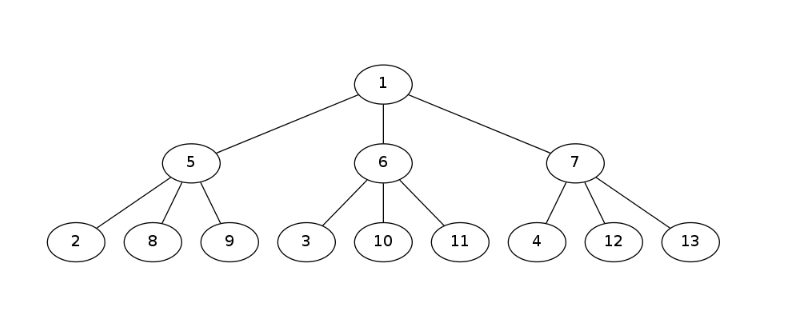
点分树源于点分治有一些很好的性质:
1、树高严格小于等于logn
2、点分树上每个点的子树中所有点就是原树中以这个点为分治中心时要遍历到的点
3、点分树上以一个点x到根路径上的每个点为分治中心时都会遍历到这个点x
4、点分树上的边不是原树上的边
那么怎么用点分树实现动态点分治呢?我们考虑点分治以某个点为分治中心时,遍历到的点组成了一个联通块,而这个联通块中的点就是这个分治中心在点分树上的子树中的所有点。点分治时每个分治中心需要遍历它所在联通块来得到它和联通块内每个点之间的信息,那么点分树上每个点就需要维护这个点和子树中每个点之间的信息。这样当修改某个点的信息时只需要更改这个点在点分树上到根路径上每个点维护的信息。而查询时也只需要查询点分树上从查询点到根路径上的每个点的信息进行统计。
这里有几个地方需要注意:
1、因为每个点要维护和子树中所有点的信息,所以一般来说每个点维护的信息需要用数据结构来维护,也就是点分树套数据结构
2、因为点分树上的边不是原树上的边,所以需要用原树两点间LCA来求两点间距离,为了不影响时间复杂度,要用RMQ求LCA
3、动态点分治统计答案一般采用容斥的方法
4、构建点分树就是跑一遍不统计信息的空的点分治
5、解决动态点分治问题时可以先考虑单次询问用点分治如何处理、需要求什么信息,然后再转到点分树上进行处理。
说了这么多来看一道例题:给一棵n个节点的树,边权为1,点有点权,有m次操作,每次操作要么修改一个点的权值,要么询问距离一个点距离小于等于k的所有点的点权和,强制在线,n,m<=10^5。
我们考虑单次询问用点分治如何处理?假设查询点为x。
1、如果当前分治联通块中没有x,那么不用再分治统计了;
2、如果当前联通块中有x并且x不是分治中心,假设当前分治中心与x间的距离为d,我们需要找到与分治中心距离<=k-d的所有点的点权和。但这样统计有不合法的点,即与x在分治中心的同一棵子树中的点,所有我们还需要统计x所在的分治中心的那棵子树中与分治中心距离<=k-d的所有点权和,将这部分答案减掉即可。
3、如果x为当前分治中心,那么直接统计当前联通块中与x距离<=k的点的点权和即可。
其实第三种情况可以归为第二种情况中,那么我们就可以得出每个点需要维护的信息(其中k为任意距离,为了方便我们称以一个点为分治中心时能遍历到的点组成的联通块为这个点管辖的联通块):
1、以当前点为分治中心时联通块中与这个点距离<=k的点权和,这个用线段树维护每个距离的点权和即可。
2、以当前点在原树上的父节点为分治中心时,这个点在原树的子树中与这个点父节点距离<=k的点权和,这个同样用线段树维护,但是我们知道当前点在点分树上无法维护这个联通块的信息,所以这个联通块的信息由这个联通块的重心的那棵线段树来维护。也就变成了每个点维护点分树上这个点子树中所有点与这个点在点分树上的父节点距离<=k的点的点权和。
那么修改就很好办了,因为一个点的点权只被这个点在点分树上到根路径上所有点保存,只要暴力往根爬然后修改沿途节点线段树中信息即可。
对于查询,因为我们只需要知道管辖的联通块中包含查询点的点的信息即可,而这些点就是查询点在点分树上到根路径上的所有点,我们依旧暴力往根爬并统计沿途点的答案即可。
动态点分治的解题过程大致就是这样,可能刚开始学有些理解不了为什么在点分树上这么做是对的,但通过做题就会慢慢理解。还要注意的是动态点分治的时间复杂度较高,因此许多题存在卡常现象,要注意常数优化。
可持久化点分树
点分树作为一种数据结构也支持可持久化,同样对于每一个版本建出一条链并将链上点没建出的子节点连向上一个版本的对应节点,但如果直接连接可能一个点会有许多儿子,这样时间复杂度就不对了,因此我们将多叉树转二叉树(具体操作详见),这样一个点的出边最多只有三个,点分树上的子节点数也就最多只有三个。现在我们来具体说说新建一个版本及查询一个版本如何实现:
和寻常的数据结构有所不同,点分树无论插入还是查询都是自下而上操作的,插入还好办,但查询时我们无法知道查询点在在当前查询版本中的位置。这就需要换一种插入和查询方式了。首先,对于原点分树记录出每个点是它的父节点的第几个儿子称为这个点的标号,并且对于每个点用一个vector记录出在点分树上它到根的路径中每个点的标号,这样我们对于一个操作点就可以从根往下地找到它了。同时可持久化点分树上每个点还要记录出这个点在原点分树上对应哪个点,因此可持久化点分树必须建出第0个版本的整个点分树即原点分树,然后每个版本再相应的建出一条链。
最后推荐几道练习题(难度由低到高,部分题卡常):
(利用点分树性质求带权重心)
(动态点分治求直径)
(上面讲的例题,非常卡常)
(动态点分治+线段树,和震波差不多)
(二分答案+动态点分治)
(动态重构点分树,替罪羊式点分树套高速平衡树,注意平衡树的选择)
(可持久化点分树)